«Информатика и ее применения» (Том 8, Выпуск 2, 2014)

Оглавление | Библиография | Об авторах

Аннотации и ключевые слова.

АНАЛИТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАСПРЕДЕЛЕНИЙ С ИНВАРИАНТНОЙ МЕРОЙ В НЕГАУССОВСКИХ ДИФФЕРЕНЦИАЛЬНЫХ И ПРИВОДИМЫХ К НИМ ЭРЕДИТАРНЫХ СТОХАСТИЧЕСКИХ СИСТЕМАХ.

• И. Н. Синицын  Институт проблем информатики Российской академии наук, sinitsin@dol.ru

Аннотация: Представлены методы и алгоритмы аналитического моделирования одно- и многомерных распределений с инвариантной мерой в дифференциальных и интегродифференциальных (эредитарных) стохастических системах (СтС), описываемых уравнениями Ито в конечномерных пространствах с винеровскими и пуассоновскими шумами. Сначала в разд. 2 рассматриваются интегродифференциальные уравнения Пугачева для распределений процессов в дифференциальных СтС (ДСтС). Применительно к ДСтС с гладкими и разрывными регулярными правыми частями найдены условия сохранения инвариантной меры для нестационарных и стационарных процессов. Сформулированы 4 теоремы, определяющие точные алгоритмы аналитического моделирования распределений с инвариантной мерой в ДСтС общего вида. В разд. 3 дан краткий обзор приближенных методов аналитического моделирования в ДСтС, основанных на параметризации распределений. Особое внимание уделено методам нормальной аппроксимации и статистической линеаризации для приближенного определения одно- и двумерных распределений с инвариантной мерой. Получены условия устойчивости алгоритмов. Сформулированы две теоремы, определяющие приближенные алгоритмы аналитического моделирования в ДСтС. Раздел 4 посвящен методам и алгоритмам аналитического моделирования распределений с инвариантной мерой в интегродифференциальных эредитарныхСтС(ЭСтС), приводимых к дифференциальным. Представлены нелинейные стохастические интегродифференциальные уравненияИто с винеровскими и пуассоновскими шумами. Для затухающих физически возможных эредитарных ядер рассматривается два способа их аппроксимации (на основе линейных операторных уравнений и вырожденных ядер). Рассмотрены три теоремы, определяющие точные и приближенные алгоритмы приведения ЭСтС к ДСтС для гладких и разрывных регулярных правых частей. В приложении даны тестовые примеры для разрабатываемого в ИПИ РАН инструментального программного обеспечения «ID StS» в среде MATLAB. Заключение содержит основные выводы и возможные обобщения. Рассмотрено применение результатов разд. 2–4 к задачам эквивалентности гауссовских и негауссовских ДСтС и ЭСтС.

Ключевые слова: аналитическое моделирование; гауссовская (нормальная) стохастическая система; дифференциальная стохастическая система; инструментальное программное обеспечение «ID StS»; метод нормальной аппроксимации; метод статистической линеаризации; негауссовская (с винеровскими и пуассоновскими шумами) стохастическая система; распределение с инвариантной мерой; сингулярное (вырожденное) ядро; стохастическое дифференциальное уравнение Ито; система, приводимая к дифференциальной; эредитарное ядро

СИСТЕМА Geo/Geo/1/R С ГИСТЕРЕЗИСНОЙ ПОЛИТИКОЙ.

• А. В. Печинкин  Институт проблем информатики Российской академии наук; Российский университет дружбы народов, apechinkin@ipiran.ru
• Р. В. Разумчик  Институт проблем информатики Российской академии наук, rrazumchik@ieee.org

Аннотация: Пороговое управление нагрузкой является одним из основных средств предотвращения перегрузок в сетях связи. Его разновидности применяются при обнаружении перегрузок как в сетях общеканальной сигнализации №7, так и в сетях связи следующего поколения, где основой сигнализа- ции служит протокол установления сессий (SIP — session initiation protocol). В работе рассматривается функционирующая в дискретном времени система массового обслуживания (СМО) Geo/Geo/1/R с двухпороговой гистерезисной политикой, представляющая собой одну из возможных математических моделей SIP-сервера с управлением нагрузкой. Предложены методы нахождения совместного стаци- онарного распределения числа заявок в системе и состояния системы, распределения времен выхода системы из множества состояний нормальной работы и множества состояний перегрузки и блокировки и их моментов, стационарного распределения времени ожидания начала обслуживания заявки. Приведены примеры численных расчетов, проведенных с помощью полученных аналитических соотношений.

Ключевые слова:  система массового обслуживания; дискретное время; гистерезисное управление нагрузкой; показатели функционирования системы

ON THE OVERFLOW PROBABILITY ASYMPTOTICS IN A GAUSSIAN QUEUE.

• O. V. Lukashenko  Institute of Applied Mathematical Research, Karelian Research Center, Russian Academy of Sciences, 11 Pushkinskaya Str., Petrozavodsk 185910, Russian Federation
  Petrozavodsk State University, 33 Lenin Str., Petrozavodsk 185910, Russian Federation
• E. V. Morozov   Institute of Applied Mathematical Research, Karelian Research Center, Russian Academy of Sciences, 11 Pushkinskaya Str., Petrozavodsk 185910, Russian Federation
  Petrozavodsk State University, 33 Lenin Str., Petrozavodsk 185910, Russian Federation
• M. Pagano   University of Pisa, 43 Lungarno Pacinotti, Pisa 56126, Italy

ОБ АСИМПТОТИКЕ ВЕРОЯТНОСТИ ПЕРЕПОЛНЕНИЯ ГАУССОВСКОЙ ОЧЕРЕДИ.

• О. В. Лукашенко  Институт прикладных математических исследований КарНЦ РАН, Россия, Республика Карелия, г. Петрозаводск 185910, ул. Пушкинская 11;
  Петрозаводский государственный университет, Россия, Республика Карелия, г. Петрозаводск 185910, пр. Ленина 33; lukashenko-oleg@mail.ru
• Е. В. Морозов  Институт прикладных математических исследований КарНЦ РАН, Россия, Республика Карелия, г. Петрозаводск 185910, ул. Пушкинская 11;
  Петрозаводский государственный университет, Россия, Республика Карелия, г. Петрозаводск 185910, пр. Ленина 33; emorozov@karelia.ru
• М. Пагано   Университет г. Пиза, Италия; m.pagano@iet.unipi.it

Аннотация: Гауссовские процессы являются мощным инструментом в моделировании сетей, так как они позволяют описать эффект долгой памяти реальных сетевых потоков. Более точно, при реали- стичных предположениях, дробное броуновское движение (ДБД) возникает как предельный процесс, когда огромное число on-off источников (с тяжелыми хвостами) мультиплексируются в магистральных сетях. В данной работе изучается жидкостная система массового обслуживания с постоянной скоростью обслуживания, с суммой независимых ДБД на входе, что соответствует агрегации гетерогенных сетевых потоков. Для таких системмассового обслуживания получена логарифмическая асимптотика вероятности переполнения, которая является верхней границей вероятности потери в соответствующих очередях с конечным буфером и которая показывает, что в оценке доминирует ДБД с наибольшим параметром Херста. Наконец, приведены асимптотические результаты для максимума нагрузки в более общем случае гауссовского входного процесса с дисперсией, которая правильно меняется на бесконечности

Ключевые слова: гауссовские жидкостные системы; вероятность переполнения; логарифмические асимптотики

ОБОБЩЕННАЯ ЗАДАЧА РАСПРЕДЕЛЕНИЯ РЕСУРСОВ ПРОГРАММНОЙ СИСТЕМЫ.

• А. В. Босов  Институт проблем информатики Российской академии наук, AVBosov@ipiran.ru

Аннотация: Представленыпостановка и решение задачи оптимизации динамической системыс линейным выходом по квадратичному критерию качества. Неопределенность системы описывается наблюдаемым случайным процессом второго порядка. В качестве практического обоснования рассматриваются потребности оптимизации распределения ресурсов некоторой программной системы. В такой интерпретации неопределенность системы описывает пользовательскую активность, а выход — число выполняемых запросов или объем запрашиваемой памяти. Цель оптимизации формализуется квадратичнымкритерием качества общего вида. Критерий, в частности, обобщает две задачи распределения ресурсов программной системы, рассмотренные ранее. Целевой функционал позволяет, в частности, ставить задачи выделения достаточного объема программных ресурсов (нитей, памяти и т. п.), штрафуя за их неограниченное расходование. Для решения задачи используется метод динамического программирования. Оптимальная стратегия находится в виде линейной комбинации выхода и прогнозов состояния вплоть до горизонта управления. В связи с вычислительной трудоемкостью оптимальной стратегии обсуждается возможность ее упрощения и применения локально-оптимальной стратегии.

Ключевые слова: программная система; стохастическая система наблюдения; квадратичный критерий; динамическое программирование

БАЙЕСОВСКАЯ РЕКУРРЕНТНАЯ МОДЕЛЬ РОСТА НАДЕЖНОСТИ:
БЕТА-РАСПРЕДЕЛЕНИЕ ПАРАМЕТРОВ .

• Ю. В. Жаворонкова  ООО КМ Медиа, juliana-zh@yandex.ru
• А. А. Кудрявцев  Московский государственный университет им. М.В. Ломоносова, факультет вычислительной математики и кибернетики, nubigena@hotmail.com
• С. Я. Шоргин   Институт проблем информатики Российской академии наук, sshorgin@ipiran.ru

Аннотация: Одной из актуальных задач современной прикладной математики является задача прогнозирования надежности сложных модифицируемых информационных систем. Любая впервые созданная сложная система, предназначенная для переработки или передачи информационных потоков, как правило, не обладает требуемой надежностью. Такие системы подвергаются модификациям в ходе разработки, опытной эксплуатации и штатного функционирования. Целью таких модификаций является увеличение надежности информационных систем. В связи с этим возникает необходимость формализации понятия надежности модифицируемых информационных систем и разработки методов и алгоритмов оценивания и прогнозирования различных надежностных характеристик. Одним из подходов к определению надежности системы является вычисление вероятности того, что на сигнал, поданный на вход системы в определенный момент времени, система отреагирует корректно. В статье рассматривается экспоненциальная рекуррентная модель роста надежности, в которой вероятность надежности системы представляется как линейная комбинация параметров «дефективности» и «эффективности» средства, исправляющего недостатки системы. Предполагается, что исследователь не имеет точных сведений об исследуемой системе, а лишь знаком с характеристиками класса, из которого берется данная система. Врамках байесовского подхода предполагается, что показатели «дефективности» и «эффективности» имеют бета-распределение. Вычисляется средняя предельная надежность системы. Приводятся численные результаты для модельных примеров.

Ключевые слова: модифицируемые информационные системы; теория надежности; байесовский подход; бета-распределение

МЕТОД ДОКАЗАТЕЛЬСТВА НАБЛЮДАЕМОЙ ЭКВИВАЛЕНТНОСТИ ПРОЦЕССОВ С ПЕРЕДАЧЕЙ СООБЩЕНИЙ.

• А. М. Миронов  Институт проблем информатики Российской академии наук, amironov66@gmail.com

Аннотация: Рассматривается проблема доказательства наблюдаемой эквивалентности для класса вычислительных процессов, называемых процессами с передачей сообщений. Действия, выполняемые такими процессами, заключаются в посылке или приеме сообщений, проверке логических условий и обновлении значений внутренних переменных процессов. Основным результатом статьи является теорема, сводящая задачу доказательства наблюдаемой эквивалентности пары процессов с передачей сообщений к задаче нахождения формул, ассоциированных с парами состояний этих процессов, удовлетворяющих некоторым условиям, которые связаны с переходами этих процессов. Данное сведение является обобщением известного методаФлойда верификации блок-схем, в котором задача верификации блок-схемы сводится к задаче нахождения формул (называемых промежуточными утверждениями), связанных с некоторыми точками в блок-схемах и удовлетворяющих некоторым условиям, соответствующим переходам в блок-схемах. Изложенный метод доказательства наблюдаемой эквивалентности процессов с передачей сообщений иллюстрируется примером верификации протокола скользящего окна.

Ключевые слова: верификация; процессы с передачей сообщений; наблюдаемая эквивалентность; протокол скользящего окна

О ПОЛИНОМИАЛЬНОЙ РАЗРЕШИМОСТИ УЛЬТРАМЕТРИЧЕСКИХ ВЕРСИЙ НЕКОТОРЫХ NP-ТРУДНЫХ ЗАДАЧ.

• М. Г. Адигеев  Южный федеральный университет, madi@math.sfedu.ru

Аннотация: Статья посвящена анализу важных частных случаев задачи коммивояжера и задачиШтейнера. Обе эти задачи являются NP-трудными даже в метрическом случае, т. е. для графов, у которых функция стоимости ребер удовлетворяет неравенству треугольника. Более строгим ограничением является уси- ленное неравенство треугольника: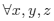
.
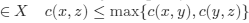Метрические функции, удовлетворяющие такому условию, называются ультраметрическими. В статье на основе анализа графов с ультраметрической функцией стоимости ребер разработан алгоритм, позволяющий построить для та- кого графа гамильтонов цикл минимальной стоимости за время 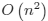, где n — число вершин графа. Для задачи Штейнера показано, что при ультраметрической функции стоимости ребер минимальное дерево Штейнера содержит только терминальные вершины и поэтому также может быть построено за полиномиальное время как минимальное остовное дерево на подграфе исходного графа.

Ключевые слова: ультраметрическая функция; усиленное неравенство треугольника; задача коммивоя- жера; деревоШтейнера; полиномиальные алгоритмы

РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ В МНОГОДИПОЛЬНОЙ МОДЕЛИ ИСТОЧНИКОВ МАГНИТОЭНЦЕФАЛОГРАММ МЕТОДОМ НЕЗАВИСИМЫХ КОМПОНЕНТ.

• В. Е. Бенинг Московский государственный университет им. М.В. Ломоносова, факультет вычислительной математики и кибернетики;
  Институт проблем информатики Российской академии наук, bening@yandex.ru
• М. А. Драницына  Московский государственный университет им. М.В. Ломоносова, факультет вычислительной математики и кибернетики, margarita13april@mail.ru
• Т. В. Захарова  Московский государственный университет им. М.В. Ломоносова, факультет вычислительной математики и кибернетики, lsa@cs.msu.ru
• П. И. Карпов   Национальный исследовательский технологический университет «МИСиС», karpov.petr@gmail.com

Аннотация: Настоящая работа посвящена изучению функциональных зон головного мозга человека. Функциональное картирование коры головного мозга является чрезвычайно сложной задачей, возникновение которой обусловлено современным уровнем развития методов неинвазивного исследования головного мозга. Магнитоэнцефалография (МЭГ), один из таких современных неинвазивных методов, — очень мощный инструмент, обладающий научным и прикладным медицинским потенциалом. Результатом проведения МЭГ являются большие массивы данных, несущие информацию о процессах, происходящих в головном мозге. В ходе обработки этих данных перед исследователем ставится некорректная обратная задача, заключающаяся в пространственной реконструкции источников МЭГ-сигналов в коре головного мозга человека с заданной точностью. На настоящий момент не существует универсальных инструментов для точного в достаточной степени решения такой обратной задачи при анализе МЭГ-сигналов. Одному и тому же распределению потенциалов на поверхности головы могут соответствовать различные зоны активности коры головного мозга. Однако при некоторых предположениях: источники потенциала дискретные, относятся к различным функциональным областям мозга, располагаются относительно неглубоко, — задача имеет однозначное решение. В данной работе предполагается, чтоМЭГ-сигнал представляет собой суперпозициюсигналов мультидиполей. Решение обратной задачи в такомслучае называетсямногодипольнымприближением. Нахождение источников активности проходит в два этапа: на первомметодомнезависимых компонент производится декомпозиция исходных МЭГ-сигналов на конечное число независимых компонент; на втором по аналитической формуле рассчитываются координаты однодипольного источника активности для каждой отдельной независимой компоненты.

Ключевые слова: метод независимых компонент; нормальное распределение; токовый диполь; многодипольная модель; магнитоэнцефалограмма

ПОСТРОЕНИЕ АГРЕГИРОВАННЫХ ПРОГНОЗОВ ОБЪЕМОВ ЖЕЛЕЗНОДОРОЖНЫХ ГРУЗОПЕРЕВОЗОК C ИСПОЛЬЗОВАНИЕМ РАССТОЯНИЯ КУЛЬБАКА–ЛЕЙБЛЕРА.

• А. П. Мотренко Московский физико-технический институт, anastasia.motrenko@gmail.com
• В. В. Стрижов  Вычислительный центр Российской академии наук им. А. А. Дородницына, strijov@ccas.com

Аннотация: Данное исследование посвящено проблеме построения агрегированных прогнозов объемов железнодорожных грузоперевозок. Для получения агрегированных прогнозов требуется кластеризовать временн‚ые ряды таким образом, чтобы распределения временн‚ых рядов внутри кластера совпадали. При решении задачи кластеризации требуется оценить близость между временн‚ыми рядами, исходя из их эмпирических распределений. Вводится критерий принадлежности временн‚ых рядов одному распределению, основанный на расстоянииКульбака–Лейблера между гистограммами временн‚ых рядов. Приводится теоретическое и практическое исследование предложенного критерия. Решается задача кластеризации временн‚ых рядов на основе матрицы парных расстояний между ними.

Ключевые слова: эмпирическая функция распределения; расстояние между гистограммами; расстояние Кульбака–Лейблера; задача двух выборок

ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ КОРПУСНЫХ ИССЛЕДОВАНИЙ: ПРИНЦИПЫ ПОСТРОЕНИЯ КРОССЛИНГВИСТИЧЕСКИХ БАЗ ДАННЫХ.

• Н. В. Бунтман  Московский государственный университет им. М.В. Ломоносова, факультет иностранных языков и регионоведения, nabunt@hotmail.com
• Анна A. Зализняк  Институт языкознания Российской академии наук;
  Институт проблем информатики Российской академии наук, anna.zalizniak@gmail.com
• И. M. Зацман  Институт проблем информатики Российской академии наук, izatsman@yandex.ru
• М. Г. Кружков  Институт проблем информатики Российской академии наук, magnit75@yandex.ru
• Е. Ю. Лощилова  Институт проблем информатики Российской академии наук, lena0911@mail.ru
• Д. В. Сичинава  Институт русского языка Российской академии наук, mitrius@gmail.com

Аннотация: Рассматривается информационная технология создания кросслингвистических баз данных текстов на русском языке и их переводов на французский язык, называемых параллельнымит екстами. Разработанные принципы построения этой базы данных обеспечивают реализацию уникального сочетания трех видов двуязычногопоиска: лексического, грамматического и лексико-грамматического. Отличительной чертой рассматриваемой технологии является одновременное формирование русско-французского параллельного подкорпуса Национального корпуса русского языка (НКРЯ) и кросслингвистической базы данных глагольных лексико-грамматических форм русского языка и их функциональных эквивалентов во французских переводах. Подкорпус и база данных обладают разной глубиной выравнивания: в первом случае оно выполняется на уровне предложений, а во втором — на уровне конструкций. Теоретическое значение создания этой базы данных заключается в обеспечении исследований как в области двуязычной контрастивной грамматики, так и в направлении создания грамматики русского языка, опирающейся на современную эмпирическую базу и информационные технологии корпусной лингвистики. Ее основное прикладное назначение заключается в повышении качества машинного перевода.

Ключевые слова: параллельный корпус; информационная технология; кросслингвистические базы дан-ых; двуязычный лексико-грамматический поиск; корпусная лингвистика; контрастивная грамматика

ПОСТРОЕНИЕ МОДЕЛЕЙ СИСТЕМНОЙ ДИНАМИКИ В УСЛОВИЯХ ОГРАНИЧЕННОЙ ЭКСПЕРТНОЙ ИНФОРМАЦИИ.

• О. Г. Кантор Институт социально-экономических исследований Уфимского научного центра Российской академии наук, o_kantor@mail.ru
• С. И. Спивак  Башкирский государственный университет, semen.spivak@mail.ru

Аннотация: Системная динамика — методология изучения сложных динамических систем, ориентированная на проведение компьютерного эксперимента. Построение моделей системной динамики во многом зависит отимеющейся экспериментальной информации и квалификации экспертов. Имитационный эксперимент с «плохими» моделями может привести к существенному или даже полному искажениюсвойств изучаемой системы. В настоящей работе приводится описание метода построения моделей системной динамики, представляющего собой комплекс математических моделей, в основу которых положены идеи подхода Л.В. Канторовича к математической обработке экспериментальных данных, и вычислительных процедур. Важным преимуществом при этом является возможность включения в модель значимых с точки зрения исследователя условий, влияющих на ее адекватность. Апробация разработанного метода осуществлялась на примере моделирования численности населения Российской Федерации.

Ключевые слова: модели системной динамики; точечные и интервальные оценки параметров моделей; подход Л.В. Канторовича; предельно допустимые погрешности измерений

ДЕКЛАРАТИВНЫЕ СТРУКТУРЫ ЗНАНИЙ В ПРОБЛЕМНО-ОРИЕНТИРОВАННЫХ СИСТЕМАХ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА.

• А. Г. Мацкевич  Институт проблем информатики Российской академии наук;
  Московский технический университет связи и информатики (МТУСИ), xmag@mail.ru

Аннотация: Описаны методы и средства представления знаний в виде декларативных структур на основе расширенных семантических сетей (РСС) для формирования баз знаний (БЗ) систем искусственного интеллекта, а также приведены примеры реализованных интеллектуальных систем обработки знаний для различных предметных областей. Для обработки декларативных структур знаний, представленных в виде РСС, разработанспециализированный язык логического программирования ДЕКЛ. На языке ДЕКЛ были реализованы лингвистические процессоры (ЛП), осуществляющие перевод предложений естественного языка (ЕЯ) (русского и английского) в структурыБЗ, а также обратный переводиз внутренних (глубинных) представлений в поверхностные формы русского или английского языка.

Ключевые слова: интеллектуальные системы; представление знаний; обработка естественного языка; семантические сети; логическое программирование

УНИВЕРСАЛЬНАЯ ТЕХНОЛОГИЯ ОЦЕНКИ БЛИЗОСТИ ИНФОРМАЦИОННЫХ ОБЪЕКТОВ.

• Л. А. Кузнецов  Российская академия народного хозяйства и государственной службы при Президенте Российской Федерации (Липецкий филиал), Kuznetsov.Leonid48@gmail.com

Аннотация: Изложена технология определения степени подобия информационных объектов, которые представлены текстами или графическими изображениями. Объекты формализуются вероятностными моделями. Структура модели задается алгеброй на минимальном наборе изобразительных компонентов объекта. Количественными характеристиками структурыобъектов являются распределения вероятностей на заданной алгебре. Количество информации в объектах оценивается энтропией. На энтропиях задается мера информационного подобия сопоставляемых объектов. Показана методика формирования оценки для текстовых и графических объектов. Приведены примеры реализации алгоритмов оценки и показана более высокая эффективность разработанных методов по сравнению с методами, описанными в лите- ратуре. Технология формирования образов информационных объектов и сравнения их семантического содержания является универсальной. Показаны возможности адаптации разработанной технологии к содержательным характеристикам исследуемых объектов.

Ключевые слова: информационный объект; текст; изображение; вероятностная модель; семантическое подобие; энтропия; мера подобия