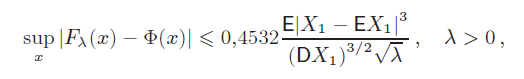«Информатика и её применения» (Том 5, Выпуск 3, 2011)

Оглавление | Библиография | Об авторах

Аннотации и ключевые слова.

АСИМПТОТИЧЕСКИ ОПТИМАЛЬНЫЙ КРИТЕРИЙ ПРОВЕРКИ ГИПОТЕЗ О ЧИСЛЕ КОМПОНЕНТ СМЕСИ ВЕРОЯТНОСТНЫХ РАСПРЕДЕЛЕНИЙ.

• В. Е. Бенинг   Московский государственный университет им. М.В. Ломоносова, факультет вычислительной математики и кибернетики; Институт проблем информатики Российской академии наук, bening@yandex.ru
• А.К. Горшенин  Московский государственный университет им. М.В. Ломоносова, факультет вычислительной математики и кибернетики; Институт проблем информатики Российской академии наук, a.k.gorshenin@gmail.com
• В.Ю. Королев  Московский государственный университет им. М.В. Ломоносова, факультет вычислительной математики и кибернетики; Институт проблем информатики Российской академии наук, vkorolev@cs.msu.su

Аннотация: Рассмотрена задача статистической проверки гипотез о числе компонент смеси вероятностных распределений. Приведен асимптотически наиболее мощный критерий. При выполнении достаточно слабых условий найдены предельные распределения, потеря мощности и асимптотический дефект. Подробно рассмотрено применение данного критерия к проверке гипотез о числе компонент смесей равномерных, нормальных и гамма-распределений.

Ключевые слова:  смеси вероятностных распределений; асимптотически наиболее мощный критерий; потеря мощности; асимптотический дефект

РЕКОНСТРУКЦИЯ РАСПРЕДЕЛЕНИЙ СЛУЧАЙНЫХ ФУНКЦИЙ В ЗАДАЧАХ ОДНОФОТОННОЙ ЭМИССИОННОЙ ТОМОГРАФИИ ПРИ ПОМОЩИ АППРОКСИМАЦИИ ЭКСПОНЕНЦИАЛЬНОГО МНОЖИТЕЛЯ ТРИГОНОМЕТРИЧЕСКИМИ МНОГОЧЛЕНАМИ.

• В. Г. Ушаков   Московский государственный университет им. М.В. Ломоносова, кафедра математической статистики факультета вычислительной математики и кибернетики; Институт проблем информатики Российской академии наук, vgushakov@mail.ru
• О.В.Шестаков  Московский государственный университет им. М.В. Ломоносова, кафедра математической статистики факультета вычислительной математики и кибернетики; Институт проблем информатики Российской академии наук, oshestakov@cs.msu.su

Аннотация: Рассмотрена задача определения вероятностных характеристик случайных функций по распределениям интегральных преобразований, возникающих в задачах эмиссионной томографии. В классе дискретных случайных функций разработан метод восстановления распределений.

Ключевые слова:  эмиссионная томография; преобразование Радона; проекции; случайные функции

ДИВЕРСИФИКАЦИЯ И ЕЕ СВЯЗЬ С МЕРАМИ РИСКА.

• Д.О. Яковенко   Гроссмейстер ФИДЕ, ms@cs.msu.su
• М.А. Целищев  Московский государственный университет им. М.В. Ломоносова, кафедра математической статистики факультета вычислительной математики и кибернетики; ms@cs.msu.su

Аннотация: Предложен новый подход к понятию диверсификации инвестиционных портфелей, которое определяется как бинарное отношение во множестве портфелей с конечным первым моментом. Показано, что это бинарное отношение является (в определенном смысле) частичной упорядоченностью.
Рассмотрены важные свойства этого определения, а также необходимое и достаточное условия сравнимости портфелей, важнейшую роль в которых играет когерентная мера риска Expected Shortfall (ожидаемый дефицит). В качестве примера приводится интерпретация диверсификации информационного риска.

Ключевые слова:  диверсификация; инвестиционные портфели; сравнение портфелей; когерентные меры риска; Expected Shortfall; информационный риск

ОЦЕНКИ УСТОЙЧИВОСТИ ДЛЯ НЕКОТОРЫХ СИСТЕМ ОБСЛУЖИВАНИЯ С КАТАСТРОФАМИ.

• А.И. Зейфман  Вологодский государственный педагогический университет; Институт проблем информатики Российской академии наук; Институт социально-экономического развития территорий Российской академии наук, a_zeifman@mail.ru
• А.В. Коротышева  Вологодский государственный педагогический университет, a_korotysheva@mail.ru
• Т.Л. Панфилова  Вологодский государственный педагогический университет, ptl-70@mail.ru
• С.Я.Шоргин  Институт проблем информатики Российской академии наук, SShorgin@ipiran.ru

Аннотация: Рассматриваются модели обслуживания, описываемые марковскими цепями с непрерывным временем в случае наличия катастроф. Получены оценки устойчивости различных характеристик таких систем. Рассмотрен пример конкретной системы обслуживания.

Ключевые слова:  нестационарные системы обслуживания; марковские модели с катастрофами; оценки устойчивости; аппроксимация предельных характеристик

ОБ ОДНОЙ СТАТИСТИЧЕСКОЙ ЗАДАЧЕ ДЛЯ СЛУЧАЙНЫХ ГРАФОВ ИНТЕРНЕТ-ТИПА.

• М.М. Лери   Институт прикладных математических исследований КарНЦ РАН, leri@krc.karelia.ru
• И.А. Чеплюкова  Институт прикладных математических исследований КарНЦ РАН, chia@krc.karelia.ru

Аннотация: Рассматриваются случайные графы Интернет-типа, т. е. графы, степени вершин которых независимы и имеют степенные распределения. С помощью методов имитационного моделирования проведено исследование возможности использования критерия согласия Пирсона для проверки гипотезы о том, что степени вершин графа одинаково распределены. Построены модели зависимости мощности критерия от объема графа и параметров распределений степеней вершин и даны рекомендации по выбору числа интервалов группирования.

Ключевые слова:  случайные графы; критерий согласия Пирсона; имитационное моделирование

СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С ОТРИЦАТЕЛЬНЫМИ ЗАЯВКАМИ, БУНКЕРОМ ДЛЯ ВЫТЕСНЕННЫХ ЗАЯВОК И РАЗЛИЧНЫМИ ИНТЕНСИВНОСТЯМИ ОБСЛУЖИВАНИЯ .

• Р. В. Разумчик   Институт проблем информатики Российской академии наук, rrazumchik@ieee.org

Аннотация: Рассмотрена система массового обслуживания (СМО), в которую поступают пуассоновские потоки положительных и отрицательных заявок. Для положительных заявок имеется накопитель неограниченной емкости. Отрицательная заявка, поступающая в систему, выбивает положительную заявку из очереди в накопителе и перемещает ее в другой накопитель неограниченной емкости (бункер). Если накопитель пуст, отрицательная заявка покидает систему, не оказывая на нее никакого воздействия. После окончания обслуживания очередной заявки на прибор поступает заявка из накопителя или, если накопитель пуст, из бункера. Длительности обслуживания заявок из накопителя и бункера имеют экспоненциальные распределения с различными параметрами. Получены соотношения, позволяющие вычислять стационарные распределения очередей в накопителе и бункере.

Ключевые слова:  система массового обслуживания; отрицательные заявки; бункер; различные интенсивности обслуживания

ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ ДИАГНОСТИКИ ПЛОСКИМ ЗОНДОМ СИЛЬНОИОНИЗОВАННОЙ ПЛАЗМЫ С УЧЕТОМ КУЛОНОВСКИХ СТОЛКНОВЕНИЙ .

• И.А. Кудрявцева   Московский авиационный институт, irina.home.mail@mail.ru
• А.В. Пантелеев  Московский авиационный институт, avpanteleev@inbox.ru

Аннотация: Сформирована математическая модель, описывающая динамику сильноионизованной плазмы с учетом столкновений заряженных частиц вблизи плоского зонда. Модель включает уравнение Фоккера–Планка и уравнение Пуассона. Предложено два подхода к решению задачи: на основе метода статистических испытаний Монте-Карло и на основе композиции метода крупных частиц и метода расщепления.

Ключевые слова:  телекоммуникационные системы; метод Монте-Карло; метод крупных частиц; метод расщепления; зонд; уравнение Фоккера–Планка; уравнение Пуассона

ИСПОЛЬЗОВАНИЕ МЕТРИК ПРИ СРАВНИТЕЛЬНОМ ИССЛЕДОВАНИИ КАЧЕСТВА РАБОТЫ АЛГОРИТМОВ СЕГМЕНТАЦИИ ИЗОБРАЖЕНИЙ.

• П.П. Кольцов  Научно-исследовательский институт системных исследований Российской академии наук, koltsov@niisi.msk.ru

Аннотация: Изучается качество работы четырех известных алгоритмов цифровой сегментации изображений. Исследование проводится на совокупности искусственных тестовых изображений, подвергаемых контролируемым искажениям при априори известном эталонном ground truth изображении. Результат работы алгоритмов сегментации сравнивается с эталонным изображением с помощью метрик, обладающих различными свойствами. Использование различных метрик для оценки качества работы алгоритмов сегментации и сравнение полученных при этом результатов позволяют более точно выяснить особенности каждого из исследуемых алгоритмов.

Ключевые слова: обработка изображений; оценка качества обработки изображений; сегментация изображений; выделение границ; энергетические методы

О НЕРАВЕНСТВАХ ТИПА БЕРРИ-ЭССЕЕНА ДЛЯ ПУАССОНОВСКИХ СЛУЧАЙНЫХ СУММ.

• В.Ю. Королев   Московский государственный университет им. М.В. Ломоносова, факультет вычислительной математики и кибернетики; Институт проблем информатики Российской академии наук, vkorolev@cs.msu.su
• И. Г. Шевцова  Московский государственный университет им. М.В. Ломоносова, факультет вычислительной математики и кибернетики; Институт проблем информатики Российской академии наук, ishevtsova@cs.msu.su
• С.Я. Шоргин  Институт проблем информатики Российской академии наук, sshorgin@ipiran.ru

Аннотация: Для равномерного расстояния между функциями распределения Ф(x) стандартной нормальной случайной величины и пуассоновской случайной суммы независимых одинаково распределенных случайных величин X1, X2, . . . с конечным третьим абсолютным моментом, где - параметр пуассоновского индекса, доказано неравенство

типа оценки Берри-Эссеена, использующее центральные моменты, в отличие от ранее известных аналогичных неравенств, использующих начальные моменты.

Ключевые слова: пуассоновская случайная сумма; центральная предельная теорема; оценка скорости сходимости; неравенство Берри-Эссеена; абсолютная константа

ОБ ОДНОЙ ЯДЕРНОЙ ОЦЕНКЕ ПЛОТНОСТИ.

• В. Г. Ушаков  Московский государственный университет им. М.В. Ломоносова, факультет вычислительной математики и кибернетики; Институт проблем информатики Российской академии наук, vgushakov@mail.ru
• Н. Г. Ушаков  Институт проблем технологии микроэлектроники и особочистых материалов Российской академии наук, ushakov@math.ntnu.no

Аннотация: Исследуется ядерная оценка плотности распределения, основанная на так называемом синк- ядре. Основное внимание уделено анализу среднеквадратической ошибки оценки при конечных объемах выборки. Рассмотрены проблемы оценивания моды и производных плотности.

Ключевые слова: непараметрическое оценивание плотности; ядерная оценка; ядро бесконечного порядка

О СКОРОСТИ СХОДИМОСТИ РАСПРЕДЕЛЕНИЯ ВЫБОРОЧНОГО АБСОЛЮТНОГО МЕДИАННОГО ОТКЛОНЕНИЯ К НОРМАЛЬНОМУ ЗАКОНУ.

• О.В.Шестаков   Московский государственный университет им. М.В. Ломоносова, кафедра математической статистики факультета вычислительной математики и кибернетики; Институт проблем информатики Российской академии наук, oshestakov@cs.msu.su

Аннотация: Полученыоценки скорости сходимости распределения выборочного абсолютного медианного отклонения к нормальному закону в общем и симметричном случае.

Ключевые слова:  порядковые статистики; выборочная медиана; абсолютное медианное отклонение; нормальное распределение; оценка скорости сходимости

УСИЛЕННЫЕ ЗАКОНЫ БОЛЬШИХ ЧИСЕЛ ДЛЯ ЧИСЛА БЕЗОШИБОЧНЫХ БЛОКОВ ПРИ ПОМЕХОУСТОЙЧИВОМ КОДИРОВАНИИ.

• А.Н. Чупрунов   Научно-исследовательский институт математики и механики им. Н. Г. Чеботарева, achuprunov@mail.ru
• И. Фазекаш  Дебреценский университет, fazekas.istvan@inf.unideb.hu

Аннотация: Рассматриваются сообщения, состоящие из блоков. Каждый блок кодируется помехоустойчивым кодом, который может исправить не более r ошибок. При этом предполагается, что количество ошибок в блоке — независимая пуассоновская величина с параметром . Кроме того, предполагается, что число ошибок в сообщении принадлежит некоторому подмножеству множества неотрицательных целых чисел. В работе получены усиленные законы больших чисел для случайной величины — числа безошибочных блоков в сообщении.

Ключевые слова:  схема размещения; условная вероятность; закон больших чисел; код БЧХ