|

«INFORMATICS AND APPLICATIONS»
Scientific journal
Volume 5, Issue 3, 2011
Content | Bibliography | About Authors
Abstract and Keywords.
AN ASYMPTOTICALLY OPTIMAL TEST FOR THE NUMBER OF COMPONENTS OF AMIXTURE
OF PROBABILITY DISTRIBUTIONS
- V. E. Bening Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University; IPI RAN, bening@yandex.ru
- A.K. Gorshenin Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University; IPI RAN, a.k.gorshenin@gmail.com
- V. Yu. Korolev Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University; IPI RAN, vkorolev@cs.msu.su.
Abstract: The problem of statistical testing of hypotheses concerning the number of components in a mixture of probability
distributions is considered. An asymptotically most powerful test is presented. Under rather weak conditions, the
limit distributions, power loss, and the asymptotic deficiency are found. The application of this test to verification
of hypotheses concerning the number of components in a mixture of uniform, normal, and gamma distributions is
considered in detail.
Keywords: mixtures of probability distributions; asymptotically most powerful test; power loss; asymptotic
deficiency
RECONSTRUCTION OF RANDOM FUNCTION DISTRIBUTIONS IN SINGLE PHOTON EMISSION
TOMOGRAPHY PROBLEMS USING TRIGONOMETRIC POLYNOMIAL APPROXIMATION
OF EXPONENTIAL MULTIPLIER.
- V.G. Ushakov Department of Mathematical Statistics, Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University; IPI RAN, vgushakov@mail.ru
- O. V. Shestakov Department of Mathematical Statistics, Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University; IPI RAN, oshestakov@cs.msu.su
Abstract: This paper deals with the problemof reconstructing probabilistic distribution of random functions from distribution
of integral transforms arising in the problems of emission tomography. The method of reconstruction is developed
for the class of discrete random functions.
Keywords: emission tomography; Radon transform; projections; random functions
DIVERSIFICATION AND ITS LINKS WITH RISKMEASURES.
- D.O. Jakovenko FIDE Grandmaster, ms@cs.msu.su
- M. A. Tselishchev Department of Mathematical Statistics, Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University, ms@cs.msu.su
Abstract: A new approach is proposed to the concept of diversification of investment portfolios which is defined as a binary
relationship in the set of portfolios with finite first moments. It is shown that this relationship is, in some sense,
a partial ordering. Important properties of such a definition are considered as well as necessary and sufficient
condition of the comparability of portfolios, based on the coherent riskmeasure Expected Shortfall. As an example,
an interpretation of the diversification of information risks is presented.
Keywords: diversification; investment portfolios; comparison of portfolios; coherent risk measure; Expected
Shortfall; information risk
STABILITY BOUNDS FOR SOME QUEUEING SYSTEMS WITH CATASTROPHES.
- A. I. Zeifman Vologda State Pedagogical University; IPI RAN; VSCC CEMI RAS, a_zeifman@mail.ru
- A. V. Korotysheva Vologda State Pedagogical University, a_korotysheva@mail.ru
- T. L. Panfilova Vologda State Pedagogical University, ptl-70@mail.ru
- S. Ya. Shorgin IPI RAN, SShorgin@ipiran.ru
/ul>
Abstract: Continuous-time Markovian queueing models with catastrophes are considered. The bounds of stability for some
characteristics of such systems are obtained. Also, a queueing example is considered.
Keywords: nonstationary queues; Markovian models with catastrophes; stability bounds; approximations for
limiting characteristics
ON A STATISTICAL PROBLEM FOR RANDOM INTERNET-TYPE GRAPHS.
- M.M. Leri Institute of Applied Mathematical Research, Karelian Research Center of the Russian Academy of Sciences, leri@krc.karelia.ru
- I.A. Cheplyukova Institute of Applied Mathematical Research, Karelian Research Center of the Russian Academy of Sciences, chia@krc.karelia.ru
Abstract: There are considered random graphs of Internet-type, i. e., graphs with vertex degrees drawn independently from
power-law distributions. By means ofMonte-Carlo simulations, a possibility of using the chi-square goodness of fit
test was investigated for verification of hypothesis that graph vertex degrees are identically distributed. There were
obtained the models of the dependency of the strength of chi-square test on the graph volume and vertex degrees
distributions parameters and recommendations on choosing the number of intervals were given.
Keywords: random graphs; chi-square goodness of fit test; simulation modeling
QUEUEING SYSTEM WITH NEGATIVE CUSTOMERS, BUNKER FOR OUSTED CUSTOMERS, AND DIFFERENT SERVICE RATES.
- R. V. Razumchik IPI RAN, rrazumchik@ieee.org
Abstract: Consideration was given to the queuing system with Poisson flows of incoming positive and negative customers. For
the positive customers, there is an infinite-capacity buffer. The arriving negative customer knocks out a positive
customer queued in the buffer and moves it to an infinite-capacity buffer of ousted customers (bunker). If the
buffer is empty, then the negative customer discharges the system without affecting it. After servicing the current
customer, the server receives a customer from the buffer or, if the buffer is empty, the bunker. The service times of
customers arriving from buffer and bunker are distributed exponentially but with different parameters. Relations
for calculation of the stationary distributions of the queues in the buffer and bunker are obtained.
Keywords: queueing system; negative customers; bunker; different service rates
APPLICATION OF THE STATISTICAL METHOD AND FINITE-DIFFERENCE METHOD FOR STRONGLY IONIZED COLLISIONAL PLASMA DIAGNOSTICS PROBLEM SOLUTION BY THE FLAT PROBE.
- I.A. Kudryavtseva Department ofMathematics and Cybernetics, Moscow Aviation Institute, irina.home.mail@mail.ru
- A.V. Panteleyev Department ofMathematics and Cybernetics, Moscow Aviation Institute, avpanteleev@inbox.ru
Abstract: A mathematical model, describing strongly ionized collisional plasma dynamics near the flat probe, is formulated.
The mathematical model includes the Fokker–Planck and Poisson equations. Two methods of getting solution are
presented. One of these methods is the Monte-Carlo method, another is the combination of the splitting method
and the Particle-In-Cell method.
Keywords: Monte-Carlo method; Particle-In-Cell method; splitting method; probe; Fokker-Planck equation;
Poisson equation
COMPARATIVE STUDY OF IMAGE SEGMENTATION ALGORITHMS PROCESSING QUALITY
ON METRIC BASE.
- P. P. Koltsov Scientific Research Institute for System Analysis of the Russian Academy of Sciences, koltsov@niisi.msk.ru
Abstract: The processing quality of four well-known digital image segmentation algorithms is under study. The set of artificial
images under supervised distortions is used with a priori given reference ground truth images. Algorithms processing
results are compared with reference images by metrics with different features. The use of different metrics for image
segmentation algorithms processing quality estimation and comparative study of the results helps to clear more
exactly the features of the investigated algorithms.
Keywords: image processing; image processing quality estimation; image segmentation; edge detection; energy
methods
ON THE BERRY–ESSEEN TYPE INEQUALITIES FOR POISSON RANDOM SUMS.
- V. Yu. Korolev Department of Mathematical Statistics, Faculty of Computational Mathematics and Cybernetics,
M.V. Lomonosov Moscow State University; IPI RAN, vkorolev@cs.msu.su
- I.G. Shevtsova Department of Mathematical Statistics, Faculty of Computational Mathematics and Cybernetics,
M.V. Lomonosov Moscow State University; IPI RAN, ishevtsova@cs.msu.su
- S. Ya. Shorgin IPI RAN, sshorgin@ipiran.ru
Abstract: For the uniform distance between the distribution function Ф(x) of the standard normal random variable and the distribution function 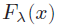 of the Poisson random sum of independent identically distributed random variables
X1, X2, . . . with finite third absolute moment, of the Poisson random sum of independent identically distributed random variables
X1, X2, . . . with finite third absolute moment, 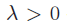 being the parameter of the Poisson index, it is proved the inequality being the parameter of the Poisson index, it is proved the inequality
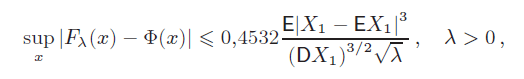
which is similar to theBerry–Esseen estimate and uses the centralmoments, unlike the known analogous inequalities
based on the noncentral moments.
Keywords: Poisson random sum; central limit theorem; convergence rate estimate; Berry–Esseen inequality;
absolute constant
ON ONE KERNEL DENSITY ESTIMATOR.
- V.G. Ushakov Department of Mathematical Statistics, Faculty of Computational Mathematics and Cybernetics, M. V. Lomonosov Moscow State University; IPI RAN, vgushakov@mail.ru
- N.G. Ushakov Institute of Microelectronics Technology and High Purity Materials, Russian Academy of Sciences, ushakov@math.ntnu.no
Abstract: The kernel density estimator based on the sinc kernel is investigated. The main attention is paid to the analysis of
the integrated mean squared for finite sample sizes (nanosymptotic). The problems of estimation of the mode and
of estimation of density derivatives are also considered.
Keywords: nonparametric density estimator; kernel estimator; kernel of infinite order
ON THE RATE OF CONVERGENCE OF SAMPLE MEDIAN ABSOLUTE DEVIATION DISTRIBUTION
TO THE NORMAL LAW.
- O. V. Shestakov Department of Mathematical Statistics, Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University; IPI RAN, oshestakov@cs.msu.su
Abstract: Some estimates for the rate of convergence of sample median absolute deviation distribution to the normal law are
obtained in the general and symmetric cases.
Keywords: order statistics; sample median; median absolute deviation; normal distribution; rate of convergence
STRONG LAWS OF LARGE NUMBERS FOR A NUMBER OF ERROR-FREE BLOCKS
UNDER ERROR-CORRECTED CODING.
- A.N. Chuprunov Department of Mathematical Statistics and Probability, Chebotarev Institute of Mathematics and Mechanics, Kazan State University, achuprunov@mail.ru
- I. Fazekas Faculty of Informatics, University of Debrecen, Hungary, fazekas.istvan@inf.unideb.hu
Abstract: The messages which contain blocks are considered. Each block was coded by error-corrected coding which can
correct not more than r errors. It is assumed that the number of errors in a block is Poissonian randomvariable with
parameter л. Also, it is assumed that the number of errors in a message belongs to a subset of nonnegative integer
numbers. Under there assumptions, the laws of large numbers for a number of error-free blocks in themessage were
obtained.
Keywords: allocation scheme; conditional probability; law of large numbers; error-corrected code
|

|