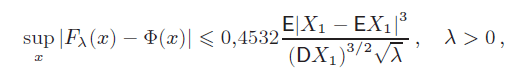“Informatics and Applications” scientific journal

Volume 5, Issue 3, 2011

Content   Abstract and Keywords   About Authors

AN ASYMPTOTICALLY OPTIMAL TEST FOR THE NUMBER OF COMPONENTS OF AMIXTURE OF PROBABILITY DISTRIBUTIONS

• V. E. Bening  Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University; IPI RAN, bening@yandex.ru
• A.K. Gorshenin  Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University; IPI RAN, a.k.gorshenin@gmail.com
• V. Yu. Korolev  Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University; IPI RAN, vkorolev@cs.msu.su.

Abstract: The problem of statistical testing of hypotheses concerning the number of components in a mixture of probability distributions is considered. An asymptotically most powerful test is presented. Under rather weak conditions, the limit distributions, power loss, and the asymptotic deficiency are found. The application of this test to verification of hypotheses concerning the number of components in a mixture of uniform, normal, and gamma distributions is considered in detail.

Keywords:  mixtures of probability distributions; asymptotically most powerful test; power loss; asymptotic deficiency

RECONSTRUCTION OF RANDOM FUNCTION DISTRIBUTIONS IN SINGLE PHOTON EMISSION TOMOGRAPHY PROBLEMS USING TRIGONOMETRIC POLYNOMIAL APPROXIMATION OF EXPONENTIAL MULTIPLIER.

• V.G. Ushakov  Department of Mathematical Statistics, Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University; IPI RAN, vgushakov@mail.ru
• O. V. Shestakov  Department of Mathematical Statistics, Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University; IPI RAN, oshestakov@cs.msu.su

Abstract: This paper deals with the problemof reconstructing probabilistic distribution of random functions from distribution of integral transforms arising in the problems of emission tomography. The method of reconstruction is developed for the class of discrete random functions.

Keywords:  emission tomography; Radon transform; projections; random functions

DIVERSIFICATION AND ITS LINKS WITH RISKMEASURES.

• D.O. Jakovenko  FIDE Grandmaster, ms@cs.msu.su
• M. A. Tselishchev  Department of Mathematical Statistics, Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University, ms@cs.msu.su

Abstract: A new approach is proposed to the concept of diversification of investment portfolios which is defined as a binary relationship in the set of portfolios with finite first moments. It is shown that this relationship is, in some sense, a partial ordering. Important properties of such a definition are considered as well as necessary and sufficient condition of the comparability of portfolios, based on the coherent riskmeasure Expected Shortfall. As an example, an interpretation of the diversification of information risks is presented.

Keywords:  diversification; investment portfolios; comparison of portfolios; coherent risk measure; Expected Shortfall; information risk

STABILITY BOUNDS FOR SOME QUEUEING SYSTEMS WITH CATASTROPHES.

• A. I. Zeifman  Vologda State Pedagogical University; IPI RAN; VSCC CEMI RAS, a_zeifman@mail.ru
• A. V. Korotysheva  Vologda State Pedagogical University, a_korotysheva@mail.ru
• T. L. Panfilova  Vologda State Pedagogical University, ptl-70@mail.ru
• S. Ya. Shorgin  IPI RAN, SShorgin@ipiran.ru /ul>

  Abstract: Continuous-time Markovian queueing models with catastrophes are considered. The bounds of stability for some characteristics of such systems are obtained. Also, a queueing example is considered.

  Keywords:  nonstationary queues; Markovian models with catastrophes; stability bounds; approximations for limiting characteristics

  ON A STATISTICAL PROBLEM FOR RANDOM INTERNET-TYPE GRAPHS.

  • M.M. Leri  Institute of Applied Mathematical Research, Karelian Research Center of the Russian Academy of Sciences, leri@krc.karelia.ru
  • I.A. Cheplyukova  Institute of Applied Mathematical Research, Karelian Research Center of the Russian Academy of Sciences, chia@krc.karelia.ru

  Abstract: There are considered random graphs of Internet-type, i. e., graphs with vertex degrees drawn independently from power-law distributions. By means ofMonte-Carlo simulations, a possibility of using the chi-square goodness of fit test was investigated for verification of hypothesis that graph vertex degrees are identically distributed. There were obtained the models of the dependency of the strength of chi-square test on the graph volume and vertex degrees distributions parameters and recommendations on choosing the number of intervals were given.

  Keywords:  random graphs; chi-square goodness of fit test; simulation modeling

  QUEUEING SYSTEM WITH NEGATIVE CUSTOMERS, BUNKER FOR OUSTED CUSTOMERS, AND DIFFERENT SERVICE RATES.

  • R. V. Razumchik  IPI RAN, rrazumchik@ieee.org

  Abstract: Consideration was given to the queuing system with Poisson flows of incoming positive and negative customers. For the positive customers, there is an infinite-capacity buffer. The arriving negative customer knocks out a positive customer queued in the buffer and moves it to an infinite-capacity buffer of ousted customers (bunker). If the buffer is empty, then the negative customer discharges the system without affecting it. After servicing the current customer, the server receives a customer from the buffer or, if the buffer is empty, the bunker. The service times of customers arriving from buffer and bunker are distributed exponentially but with different parameters. Relations for calculation of the stationary distributions of the queues in the buffer and bunker are obtained.

  Keywords:  queueing system; negative customers; bunker; different service rates

  APPLICATION OF THE STATISTICAL METHOD AND FINITE-DIFFERENCE METHOD FOR STRONGLY IONIZED COLLISIONAL PLASMA DIAGNOSTICS PROBLEM SOLUTION BY THE FLAT PROBE.

  • I.A. Kudryavtseva  Department ofMathematics and Cybernetics, Moscow Aviation Institute, irina.home.mail@mail.ru
  • A.V. Panteleyev  Department ofMathematics and Cybernetics, Moscow Aviation Institute, avpanteleev@inbox.ru

  Abstract: A mathematical model, describing strongly ionized collisional plasma dynamics near the flat probe, is formulated. The mathematical model includes the Fokker–Planck and Poisson equations. Two methods of getting solution are presented. One of these methods is the Monte-Carlo method, another is the combination of the splitting method and the Particle-In-Cell method.

  Keywords:  Monte-Carlo method; Particle-In-Cell method; splitting method; probe; Fokker-Planck equation; Poisson equation

  COMPARATIVE STUDY OF IMAGE SEGMENTATION ALGORITHMS PROCESSING QUALITY ON METRIC BASE.

  • P. P. Koltsov  Scientific Research Institute for System Analysis of the Russian Academy of Sciences, koltsov@niisi.msk.ru

  Abstract: The processing quality of four well-known digital image segmentation algorithms is under study. The set of artificial images under supervised distortions is used with a priori given reference ground truth images. Algorithms processing results are compared with reference images by metrics with different features. The use of different metrics for image segmentation algorithms processing quality estimation and comparative study of the results helps to clear more exactly the features of the investigated algorithms.

  Keywords:  image processing; image processing quality estimation; image segmentation; edge detection; energy methods

  ON THE BERRY–ESSEEN TYPE INEQUALITIES FOR POISSON RANDOM SUMS.

  • V. Yu. Korolev  Department of Mathematical Statistics, Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University; IPI RAN, vkorolev@cs.msu.su
  • I.G. Shevtsova   Department of Mathematical Statistics, Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University; IPI RAN, ishevtsova@cs.msu.su
  • S. Ya. Shorgin  IPI RAN, sshorgin@ipiran.ru

  Abstract: For the uniform distance between the distribution function Ф(x) of the standard normal random variable and the distribution function 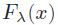of the Poisson random sum of independent identically distributed random variables X1, X2, . . . with finite third absolute moment, 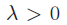being the parameter of the Poisson index, it is proved the inequality
  
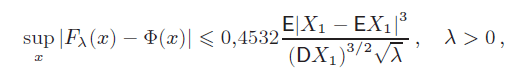
  which is similar to theBerry–Esseen estimate and uses the centralmoments, unlike the known analogous inequalities based on the noncentral moments.

  Keywords:  Poisson random sum; central limit theorem; convergence rate estimate; Berry–Esseen inequality; absolute constant

  ON ONE KERNEL DENSITY ESTIMATOR.

  • V.G. Ushakov  Department of Mathematical Statistics, Faculty of Computational Mathematics and Cybernetics, M. V. Lomonosov Moscow State University; IPI RAN, vgushakov@mail.ru
  • N.G. Ushakov  Institute of Microelectronics Technology and High Purity Materials, Russian Academy of Sciences, ushakov@math.ntnu.no

  Abstract: The kernel density estimator based on the sinc kernel is investigated. The main attention is paid to the analysis of the integrated mean squared for finite sample sizes (nanosymptotic). The problems of estimation of the mode and of estimation of density derivatives are also considered.

  Keywords:  nonparametric density estimator; kernel estimator; kernel of infinite order

  ON THE RATE OF CONVERGENCE OF SAMPLE MEDIAN ABSOLUTE DEVIATION DISTRIBUTION TO THE NORMAL LAW.

  • O. V. Shestakov  Department of Mathematical Statistics, Faculty of Computational Mathematics and Cybernetics, M.V. Lomonosov Moscow State University; IPI RAN, oshestakov@cs.msu.su

  Abstract: Some estimates for the rate of convergence of sample median absolute deviation distribution to the normal law are obtained in the general and symmetric cases.

  Keywords:  order statistics; sample median; median absolute deviation; normal distribution; rate of convergence

  STRONG LAWS OF LARGE NUMBERS FOR A NUMBER OF ERROR-FREE BLOCKS UNDER ERROR-CORRECTED CODING.

  • A.N. Chuprunov  Department of Mathematical Statistics and Probability, Chebotarev Institute of Mathematics and Mechanics, Kazan State University, achuprunov@mail.ru
  • I. Fazekas  Faculty of Informatics, University of Debrecen, Hungary, fazekas.istvan@inf.unideb.hu

  Abstract: The messages which contain blocks are considered. Each block was coded by error-corrected coding which can correct not more than r errors. It is assumed that the number of errors in a block is Poissonian randomvariable with parameter л. Also, it is assumed that the number of errors in a message belongs to a subset of nonnegative integer numbers. Under there assumptions, the laws of large numbers for a number of error-free blocks in themessage were obtained.

  Keywords:  allocation scheme; conditional probability; law of large numbers; error-corrected code